|
Internal
Waves I
References:
References for Lesson 2
Images in this lesson:
(Resizable pop-ups)
ASA_WSM_1P~ 20040128~.N1
Bathymetric map of the Mozambique study area
(17K)

Useful information:
(Resizable pop-ups)
What are internal waves?
Solitons: Solitary internal waves
(Theory and equations)
Identification of internal wave trains and their direction of propagation
IW signatures in low wind and the presence of surface films
|
SAR images of internal waves make it possible not just to identify regions of internal waves,
but also to provide quantitative estimates of IW parameters such as wavelength.
Here we will show you how to obtain this information from the images.
Notes:
1. To carry out the calculations below you will need to work with a spreadsheet or pocket calculator alongside Bilko.
The activities assume that you have a basic knowledge of how to operate these to carry out simple calculations.
2. At the start of this lesson you should have two images open:
An extract from the ASAR_WSM image from the Mozambique shelf , which you saved as
asawsm_moz28_ext.dat in the previous section, and the same image to which a
5x5 mean filter has been applied, and which you saved as asawsm_moz28_5b5_ext.dat.
Using transects to calculate wavelength
Activate the image “asawsm_moz28_5b5_ext.dat” .
Note:
If you use a linear stretch for this exercise, it will be easier to see what you are doing.
Right-click on the image, choose 'Redisplay' from the pop-up menu, and change stretch the from 'Gaussian' to 'Linear'.
Working at a zoom of 100-150% will make it easier to be accurate. Right-click on the image,
choose 'Zoom' from the pop-up menu and set the zoom to either 100% or 150%, according to preference.
To calculate the wavelength you must first create a transect that crosses two wave crests at right angles.
You could choose to do this in a number of places along the crest;
the start coordinates suggested below are chosen because this is a section where two crests are
clear and close to parallel.
-
Open the 'Go-to' dialogue and make sure sure it is set to 'line selection'.
-
Set pixel position to [210,750] and selection size to DX = 80 and DY = -72.
-
Open a new transect document for this line (right-click on the image or type [CTRL+N] ),
and select 'TRANSECT Document' from the pop-up menu.
-
Save the transect document as profile_moz28a.tsc) .
-
Place your cursor on the first peak in the transect (the first crest).
-
In the 'View' menu, ucheck 'Coords' ( [CTRL+V] > [O] )
to display the [x,y] coordinates rather than [lon,lat]. Make
a note of the [x1 ,y1 ] position of the pixel that corresponds to this peak, as shown on the Bilko status bar
(figure
(5K)).
-
Place your cursor on the second peak in the transect, and make a note of the [x2 ,y2 ] coordinates of the pixel corresponding to this peak.
Having obtained the coordinates for the two peaks, you can now use them to calculate the wavelength,
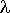 : :
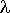 = = 
where dx = (x2 - x1),
and dy = (y2 - y1). Here
[x1,y1] is the coordinates of the first peak,
[x2,y2] are the coordinates of the second peak,
and the pixel width and pixel length are both 75m.
There is some inaccuracy involved in drawing a perpendicular transect by eye, especially when the crests are not
completely straight, and at an angle. For this reason it is worth making three calculations based on three slightly
different transects. Repeat the exercise above using the same start pixel coordinates and the following DX, DY values for the
selection size in the 'Go To' dialog:
-
DX = 80, DY = -80
-
DX = 80, DY = -73
-
DX = 80, DY = -70
|
Question 1.
|
| a) |
What are the 4 crest lengths calculated from these transects?
|
| b) |
Which of the three transects do you think is closest to being perpendicular to the wave crests at this point?
|
| c) |
If you were to calculate the wavelength at the point where the crest curves most sharply,
would it be shorter or longer than the wavelength you have just calculated?
|
Save the three remaining transects as profile_moz28*.tsc , where * represents
b, c or d.
Finally it is worth comparing transects from the filtered image with a transect from the unfiltered data.
-
With the filtered image active, select 'Connect' from the 'Image' menu (right-click on the image and choose 'Connect' from the pop-up menu,
or type [ALT+I] > [C] ) to open the 'Connect' dialogue
(figure
(4K)).
-
Select both the filtered and unfiltered image and check the 'Stack' box to display them on top of each other rather than side by side.
-
Use the 'Go-to' dialogue with 'Line selection' to redraw one of the transects you created earlier.
-
Open a new transect document to represent this line.
-
Save the new transect as profile_moz28e.tsc.
| |
|
Question 2.
|
| a) |
Which of the lines in the new transect represents the filtered data, and which the unfiltered data?
|
| b)
|
Compare the two transect lines and use your comparison to explain why it is useful to apply a filter before using transects to obtain
internal wave parameters such as wavelength.
|
Rank ordering of non-linear waves
As you can see from this image internal waves often travel in groups of several crests. These often change in wave length
and amplitude from the leading creast towards the edge of the wave train. This is known as rank ordering.
-
With the filtered image active, draw a transect across the wave group. Start ahead of the leading crest
in the middle where the wave curves most sharply, and continue past the end of the wave group to the area where no
further dark and light bands are seen
(figure
(15K)).
-
Open a new transect document.
|
|
Answers:
(Resizable pop-ups)
Answer 1
Answer 2
Answer 3
Back up to:
Q1
Q2
|
The IW signal contrast is the difference in signal strength between the brightest part of the bright
band and the darkest part of the dark band, divided by the average of these two. The contrast is related to the amplitude of
the internal wave, but this relationship is complex, so we will not attempt to calculate IW amplitude here, just note that
in a particular image, stronger contrast usually indicates a greater amplitude of the IW.
| |
|
Question 3.
|
| a) |
How does the contrast change as you move along the transect from the leading crest towards the back of the wave train?
|
| b)
|
How does the wave length change as you move towards the back of the wave train?
|
The pop-up on
Solitons: Solitary internal waves
explains how this occurs.
Next you will be using a different ASAR image from the Mozambique coast to calculate internal wave velocity. Close all the files you have
open so far, and move on.
|











 :
:

